여러 그래프를 우리가 다루게 되는데
기본적인 포물선, 원, 직선
같은 easy한 애들도 있지만
오늘은 절댓값이 포함된 함수의
그래프는 어떻게 그릴지 생각해보자.
젤 기본적인 y=|x|부터

여러분 우리 절댓값 이 자식
별로 안 좋아하잖아요?
문제에 나오면 괜히 내가 절대
풀 수 없을거 같고...
일단 꼭 우리 옆에 저 짝대기를 없애봅시다.
틀리더라도 짝대기를 정리한 후에
이건 못 푸는 문제구나~
풀 수 있는 문제구나~ 판단하기.
일단 다시 돌아와서 x=0을 기준으로
그래프가 달라지네?를 봤다면 끝.

x=0(y축)을 기준으로 xy평면이
2개의 영역으로 나눠졌고
그러면 총 2개의 그래프가 그려지겠다!
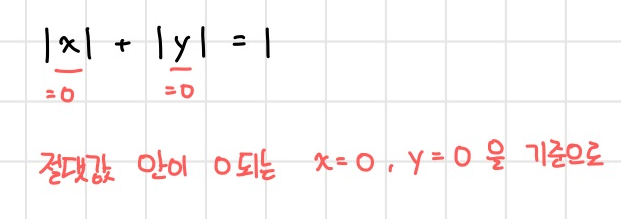
이번에는 절댓값이 2개로 늘어나면서
각각의 절댓값이 2가지로 벗겨질 수 있고
그러면 총 4가지의 경우가 나오겠다!!

그래프 자체를 뚝딱 그릴 수 있겠지만
일단 처음 그리니까 오늘은 영역에
따라서 함수가 어떻게 되는지 살펴봅시다.

x=0, y=0이 xy평면을 총 4개의 영역으로
나누고 있고 그 4개의 영역에서 각각의
그래프가 그려지겠다!!!
생각보다 easy하죠
절댓값은 대칭성을 가지면서 그래프가 그려지는구나?
나중에 처음 보는 친구가 나와도
절댓값 벗겨서 한 줄 잘 이어주면
나머지도 대충~ 이어 붙이면
답이 짠하고 나올수도 있다!
(아니다 이건 너무 야매같다, 하지마)

이 놈은 특이하게
영역을 나누는 기준이 y=x, y=-x라는
우리한테 익숙한 직선이 나누고 있는거죠!
근데 앞에서 x, y축을 기준으로
절댓값이 벗겨질 때는
그냥 직접 함수를 우리가 구해보긴 했는데
얘는 기준이 y>x같이 되니까 머리가 아프네요.
그럴 때!!
그 영역의 점을 그냥 대입해 보는거죠
4개의 영역중에 오른쪽 영역에서
절댓값 두 개가 각각 어떻게
정리될지 알아보기 위해서
(1,0)을 대입하는거에요!
그걸 대입했을 때,
양수면 +로 정리하고
음수면 -로 정리하는거죠!
나중에 또 유용하게
이용할 일이 나오길
'수학 > 미적분' 카테고리의 다른 글
| 뉴턴-랩슨법(Newton's method)+문제(활용) (2) | 2024.03.05 |
|---|---|
| 동경과 접선이 이루는 각 (0) | 2024.02.23 |
| 실수의 대소관계[미분응용] (1) | 2024.02.13 |
| M급수 기출문제[편입수학] (1) | 2024.02.08 |
| M급수[복잡한 함수에서] (1) | 2024.02.07 |



