분모가 인수분해 되는
분수함수를 좀 더 이쁘게 정리할 수 없을까?
오늘은 그걸 정리해보자.
일단 다항식/다항식 형태로 이루어져 있을텐데,
지금부터 하는건 분자가 분모보다 차수가
낮아야해요 여러분.
차수가 같거나 높으면 다항식 나누기를
통해서 차수를 낮춘 후에 지금부터 하는걸
해주면 됩니다!
부분분수를 그냥 보기 좋으라고 하는건 아니고
적분을 못하걸랑요? 근데 부분분수를
해주면 내가 적분할 수 있는 형태가 됩니다!
나중에 라플라스 역변환 때문에
쓰기도 하는데 일단은 적분하려고 한다~

벌써 이쁘다. 가장 간단한 1차-1차로 인수분해된 형태

이게 이 놈의 부분분수 최종형태입니다!
이 형태에서 a, b 찾기를 유도해볼게요

a를 분자로 가지는 그 분모를 최종형태의
양변에 곱하고 분모가 0되는 값을 대입했더니
a=이라고 이쁘게 정리가 된다!!!

같은 과정을 b를 분자로 가지는 녀석으로
똑같이 해주면 b=을 얻어낼 수 있고

우리는 이렇게 기억해두면 되겠다!

한 문제 풀어보면

어렵지 않죠?
자기 분모를 가리고 그 분모가 0되는 값을 대입!

이번에는 인수분해를 했더니 완전제곱이 있을 때,

이게 이 형태의 부분분수 최종형태인데,
이상하죠. 분모가 완전제곱인 항의 분자가 외
1차가 아니라 상수냐~

이런 이유에서 그렇습니다.
분모가 2차니 분자를 1차로 잡은게 틀렸다기 보다는
저 상태는 아직 적분이 가능한 형태가 아니거든요?
그래서 어차피 이 과정을 통해서 정리를 해줘야 하니까.
최종형태를 싹다 상수를 분자로 가지는 형태로
바로 가는거죠!

1번 유형에서 했던대로 해보려고 하니
완전제곱 항의 1승만 곱했을 때는
대입을 할 수가 없네?

근데 완전제곱 전체를 곱해주는건
1번과 같은 과정으로 증명이 됩니다!

일차인 항도 마찬가지!
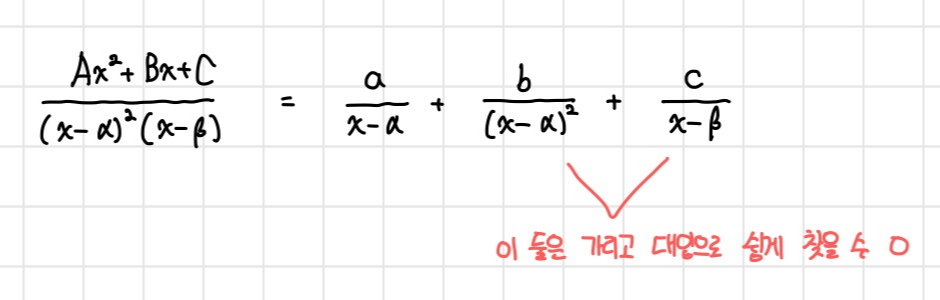
자기 분모 가리고 대입하는게 젤 쉽잖아요 여러분?
항상 그걸로 찾을 수 있는 항은
바로 찾아두시고 나머지 처리하시면 됩니다.
이제 a를 찾으러 가보면

최종형태에서 내가 다시 통분을 해주고
원래 주어진 식으로 돌아간다는 생각을 해보면
좌변과 같은 값이 나와야겠죠?
그 때, 2차항이 어디서 나올 수 있는지
이해하시면 편합니다.
지금 문자가 잔뜩 있어서 그렇지
실제로 풀어보면 a, b, c 중에서 2개는 이미
값으로 나와있어서 눈으로 찾을 수 있습니다.


빠르게 이 두개는 찾아두고
복잡해 보이던거 처리하러 가면

이렇게 4, 13이라는 값이 있으니 쉽게 찾을 수 있고
이 과정을 눈으로 해주시면 굉장히
호다닥 끝나있을거에요.
이제 마지막 유형

이번에는 완전제곱이 아닌
애초에 2차인 놈이 하나 있을 때!

가리고 대입하는 방법으로 유도를 할 수 없는
분수함수가 한 덩이리 생긴거죠!
왜냐면 그 분모가 0되는 값을 대입해서 풀었었는데
이 놈은 =0을 만족하는 실수가 없어요!

그러면 2차항 있는건 내버려두고
일단 1차항은 우리가 계속 했던 가리고 대입을
써먹을 수 있겠다!!

이 형태도 일단 가리고 대입으로
미지수 하나 줄여두고
나머지 찾으러 가보면
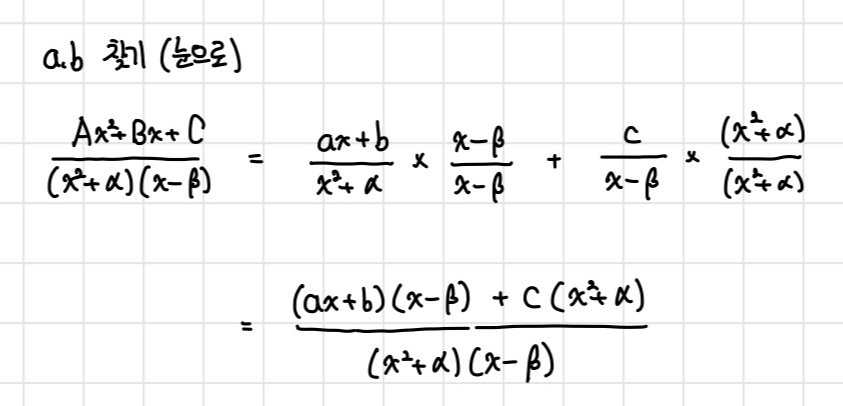
아까처럼 통분을 생각해봅시다.
2번에서 했던거 또하는건데
아까는 한 번만 했고 이번에는 a, b 두개를
그렇게 찾아줘야하는 차이입니다.

문자가 너무 많다... 별로네
일단 어떻게 하는구나~ 이 느낌만 챙기고
문제로 풀어봅시다


여기까지는 사뿐하고

둘을 만약 통분한다면
2차항이 뭐가 뭐가 나오겠구나!
그 둘이 합쳐져서 좌변에 있는 2차항과 같아야겠다

이번에는 그 과정을 상수항을 보면서 해주시면 됩니다.
이런거 다 외우지말고
한 번만 이해해보자~ 가리고 대입으로 찾을 수 있는게
뭐겠다! 나머지는 내가 눈으로 통분을 해보자.
마지막 사진 2장에서 검은색 부분을 적지않고
파란색 글씨만 적으면서 해보면
금방 익숙해질거에요!
'수학 > 미적분' 카테고리의 다른 글
| 극한 + 정적분과 무한급수[편입수학 기출문제] (3) | 2024.12.20 |
|---|---|
| 파푸스 회전체 부피[축이 직선일 때] (1) | 2024.10.13 |
| 간단해 보이는 적분 (5) | 2024.03.12 |
| 뉴턴-랩슨법(Newton's method)+문제(활용) (2) | 2024.03.05 |
| 동경과 접선이 이루는 각 (0) | 2024.02.23 |



