lim이라는 표현이 등장하는
극한파트~
극한값이란 무엇일까.
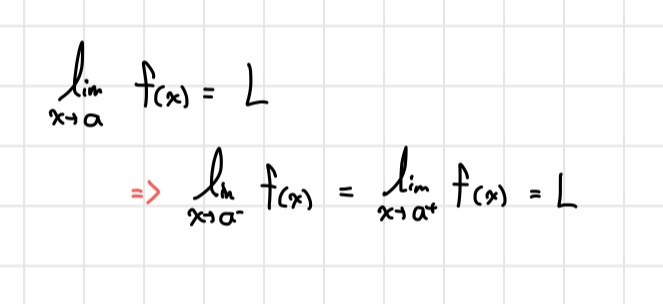
f(x)의 극한값이 L (x가 a로 갈때)이라는 말은
x가 a로 갈 때, 좌극한 = 우극한을 나타낸다.
그럼 매번 이걸 따지고 있어야하냐?
그건 또 아니지.
귀찮게 그걸 언제 다 한담.
대표적으로 절댓값, 가우스, 역삼각함수, 지수가 분수함수
일 때 생각하고
그 외에는 빠르게 확확 판단해주면 된다.
다항식일 때는 고냥 대입시켜 버리자 머리아프다.

극한값에서 주의해야할 부분은
limf(x)의 이름이 극한값이고 f(a)의 이름은 함숫값이다!
이 둘은 전혀 다르다~
'리미트'는 x가 a를 향해서 가곤 있지만 도착하지 않았다!
어어어엄청 거의 도착 했는데 그래도
딱 도착하진 않았다.
약속시간이 3신데 초침이 12에 도착한거 같은데
도착하지 않은 그런 느낌?
위 사진에서
1번 = 2번이 성립할 때, 우리는 f(x)가 x=a에서 연속이라고 한다!
- 그러니까 보통 막 같다라고 문제를 풀어도 틀릴 경우는 잘 없긴한데...
그 둘이 다르다는건 알고 있어야한다 이런 느낌? 이상한 말같네
극한 문제 중 23년에 우극한 좌극한, 절댓값 등을 이용해서
출제되었던 문제 2문제 정도만 살펴보자.

이 문제의 경우 극한값 두 개를 줄테니까 뒤에 있는 놈 극한값을 찾자!
이런 느낌의 문제
그러면 우리가 생각해야될 부분은
뒤에 있는 f(g(x)) 합성함수 형태에 대해
x가 주어진 극한으로 갈 때, g(x)가 어디로 가는지
판단만 잘 하면
주어진 조건에서 가져다 대입하면 되는 문제!
근데 그냥 극한이 아니라 좌극한, 우극한을 따질 땐
저는 그래프가 편합니다!(단호)

그래프를 생각해서 x가 극한으로 가고 있을 때,
y값이 어디로 가고 있는지 생각하고
이 문제는 단순히 값도 값이지만 +-까지 생각을 해줘야한다.
1. 파란색 화살표가 x축 아래로 올라가니 0은 0인데 -0으로 가고 있고
2. 파란색 화살표가 x축 위에서 내려가니 0은 0인데 +0으로 생각해주면
앞에서 값을 넣어주면 끝!

이 문제는 위에 문제보다는 좀 더 쉬운 문제.
일단 분자는 그냥 다항식이니까 대입해줘서 0인거 확인 끝.
다항식일 때, 극한은 편하게 편하게 생각해버리자
분모에 있는 절댓값이 문제인데
절댓값의 핵심은 뭐다? 양 옆에 있는 짝대기만 없애주면
간단한 문제가 된다.
저 짝대기를 없애주기 위해서 우리는 x가 1의 좌극한으로 갈 때
y값이 어떻게 되는지 생각해주자.

이렇게 정리만 해주면
로피탈 써도 되고, 분모에서 x^2 묶어서 정리해줘도 되는
간단한 문제!
또 분모를 조금만 더 살펴보면
절댓값은 | f(x) | 에서 f(x)가 양수냐 음수냐에 따라서
+-로 벗겨지는게 다른 부분인데
주어진 함수에서 x^2을 묶어준다면 x^2은 항상 양수이고
그러므로 부호에 영향을 주지 않아 그냥 꺼내준 후에
|x-1|에서 x가 1보다 작은 값을 대입하면 음수네?
-붙여서 꺼내야지~ 이렇게 생각하는게 좀 더 easy
'수학 > 미적분' 카테고리의 다른 글
| 삼각함수 합성 (0) | 2024.01.23 |
|---|---|
| M급수 문제유형[극한] (1) | 2024.01.22 |
| M급수 문제유형[편입수학] (0) | 2024.01.19 |
| 부정적분 형태 예상하기 (0) | 2023.08.15 |
| 미적분 기본공식 (0) | 2023.08.04 |



