728x90
반응형

일단 주어진 f(x)를 적분 안에 넣어서
어떤 모양이 만들어질지 예상해보자
+ f'(0)이 결국 미분해서
x자리에 0을 넣는다는게 1차항의 계수를 뜻한다~
a만 잘 찾으면 된는 문제!
f(0)은 상수항, f''(0)은 2차항의 계수

일단 x^3은 굳이 생각할 것도 없이
벗겨지니까 그 놈을 벗겨놓고 생각해보자

벗겨봤더니 빨간 밑줄은
적분하면 유리함수가 나오니까
지금 문제에서 큰 영향은 없다!
뒤에 있는 지저분한 놈을 적분했을때
유리함수가 나오도록 해보자
분모의 형태를 보고
부분분수의 최종적이 형태를 예상할 수 있고
그 상태에서 어떤 놈이 적분하면 유리함수가 되고
어떤 놈이 유리함수가 안 되는지 따져보자

미지수를 a부터 적고 싶었지만...
이미 문제에 a가 있으니까 b부터!
결과를 봤을 때
파랑 동그라미 두 개는 적분했을 때 ln이 나온다.
유리함수를 적분했을 때
분자가 1차이면 ln이 나오기 때문에
이 문제에서는 그 놈들이 안 생기게
a의 값을 잘 조절해봐라~
그러면 저 두 개가 없는 최종형태에서
다시 통분을 했을 때, 문제에서 주어진 f(x)가 나오는
a를 찾자.
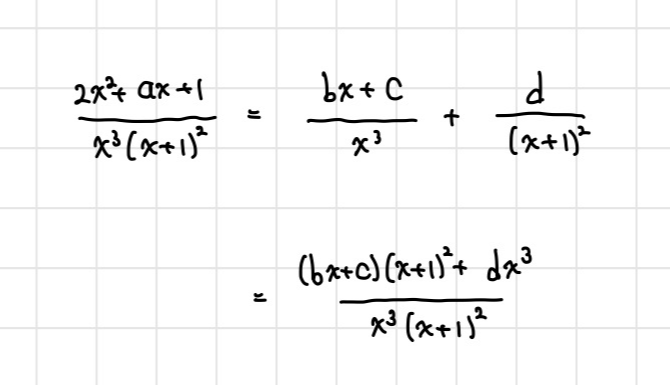

항들을 다 적어놔서 더럽지
부분분수할 때 처럼 결과를 예상하면서 하면
상수항을 보고 c=1인걸 알 수 있고
그 다음에 2차항을 보고 b값도 알아낼 수 있다!
우리는 1차항의 계수 a만 잘 찾으면 되니까
굳이 d까지 찾지 않고 문제는 끝.
최근에 출제된 세종대학교 기출문제
단순히 적분하는게 아니라
부정적분했을 때 형태를 예상해봐라~
이런 느낌의 문제
728x90
반응형
'수학 > 미적분' 카테고리의 다른 글
| 삼각함수 합성 (0) | 2024.01.23 |
|---|---|
| M급수 문제유형[극한] (1) | 2024.01.22 |
| M급수 문제유형[편입수학] (0) | 2024.01.19 |
| 함수의 극한값, 함숫값 (1) | 2024.01.17 |
| 미적분 기본공식 (0) | 2023.08.04 |



