역행렬은 어떻게 구하는걸까?
2x2행렬의 역행렬은
대각성분 자리 바꾸기, 나머지 -붙이기
이렇게 일반화된 공식이 있다보니
그렇다 쳐도. 3x3, 4x4까지 우리가 구해야 한다면?
4x4 누가 구하라고 그러면
인상쓰고 책상 엎으세요 >.<

일단 역행렬이 뭔지 살펴보면
이런 식이 나옵니다.
adjA라는 수반행렬을 구해줘야 하는데,
이 녀석이 아주 까다롭습니다.
여기서 또 하나 볼 수 있는거
역행렬을 구할 때, 1/|A|가 있다보니
|A|=0이 되면 역행렬이 존재할 수 없게 되는겁니당

여기서 여인수 어쩌고 저쩌고
머리아픈데 쉽게 가면
nxm성분을 찾기 위해서
원래 행렬에서 mxn 성분에서 십자가를 긋고
남은 놈들로 행렬식! 그런 후에 +- 고려해주기.
이 순서로 기억해주시면 됩니다.

2x2행렬의 경우
십자가를 그어버리면 남아있는게 딱 하나 일거에요.
그래서 그걸 그대로 적으면 끝.
추가로 부호만 결정해주면 되기때문에
이 놈은 간단하게 대각성분 자리바꾸기.
나머지 자리 -붙이기
이렇게 공식화 된게 있는거죠~

이건 너무 간단하고
3x3으로 가봅시다.
3x3까지는 우리가 호다닥 구할 수 있게 하는게 좋아요.
할 만 하거든요? 레츠고

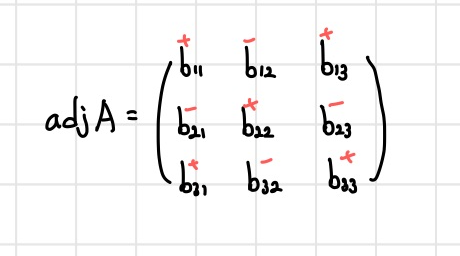
여기서부터는 전 +-부호를
행렬식할 때 고려하지 않을거에요.
그냥 빨리 십자가 긋고 행렬식을 구한 후에
adjA에 적어줄 때, +- 고려하는걸 좋아합니다.
뭔가 머리가 덜 피곤한 느낌?


3x3이 할만하다고 한 이유는
그래도 십자가를 그으면 나오는게
2x2행렬식이라서 이 정도는 우리가 눈으로 할 수 있잖아요?
그래서 할 만 합니다.
+- 마지막에 고려하자고 한 이유는
2x2행렬식이 쉽다고 해도 9개나 해야하다 보니
한 번에 고려할라고 하면 실수가 많아지는 느낌?
3x3을 보면 왜 4x4가 답도 없는지 알겠죠?
4x4는 십자가 그으면 3x3행렬식이 나오는데
3x3은 행렬식 성질을 이용해서
정리를 좀 하고 값을 찾아야하다보니 힘든거죠...ㅜㅠ
눈으로 하기에 좀 무리.
옆에 따로 3x3행렬식을 적어가면서 구해야하고
그걸 16번 해야합니다...
대학시험이면 시험 시간이 기니
뭐 한 번 손대보겠는데,
편입시험에서 4x4 역행렬의 특정 성분을 구하라는게 아니라
싹다 구하라고 그러면 조용히 X치고 다음 문제 풀고 옵시다.
시간만 투자하면 맞출 수 있는 문제는 맞는데,
효율이 좀 별로니까?

짜잔 4x4는 요렇게 됩니다!
오늘은 수반행렬 구하는걸 적어보는게
목적이라 수반행렬 성분 이야기만 잔뜩 했는데,
실제로 역행렬을 구하라고 하면
행렬식을 먼저 구해두고 가셔야합니다.
요건 알죠?
이 포스팅은 쿠팡 파트너스 활동의 일환으로
이에 따른 일정액의 수수료를 제공받습니다.
'수학 > 선형대수' 카테고리의 다른 글
| 점과 직선 사이의 거리 (0) | 2024.05.17 |
|---|---|
| 평행육면체 부피[스칼라 삼중곱] (0) | 2024.04.25 |
| 특이한 정사영문제[다항식공간, 내적을 적분으로] (0) | 2023.09.05 |
| 다항식 벡터공간의 선형변환 (0) | 2023.08.22 |
| 행렬 A의 100승 (0) | 2023.08.21 |



