미적분할 때는 입체의 부피를
x축이나 y축으로 곡선을 회전했을때
만들어지는 입체의 부피를 구하거나
단면의 모양을 알 때
단면의 넓이를 싹 더하면 부피가 되겠다~는
개념으로 부피를 구했었는데
오늘은 이중적분으로 입체의 부피를 구해보자.
암꺼나 구하는건 아니고
y라는 함수를 dx로 적분했더니
x축과 y라는 함수 사이의 넓이가 나왔다.
z라는 함수를 dydx로 적분하면
xy평면과 z라는 함수 사이의 부피가 나온다!
차원이 하나 넓어진 느낌?

이중적분하면 젤 자주 보는
너무 익숙한 두 곡면부터

문제에서 말하는 영역은 검은색으로 체크한 부분!
이 놈을 내가 위에서 바라봤을 때
xy평면에 어떤 모양이 나올지를 알아야하는데
저 곡면은 z에 숫자를 대입하면
매번 원의 방정식이 나오니까
원의 모양이 나올거 같은데 우린 반지름도 알아야하니까
찾아보자.

이렇게 z를 같다고 두면
어렵지 않게 구할 수 있는데
사실은 대충 x^2+y^2에 값을 눈으로 넣어보면
생각보다 어렵지않게
z값이 같아지는 값을 알아낼 수 있다.

영역에서 위에 있는 z랑 아래에 있는 z랑
헷갈리지 않게 조심하기!
생각보다 곡면의 형태에 따라서
헷갈리는 경우가 있다!
적분하는 함수에 x^2+y^2도 있고
영역이 원으로도 나왔으니
빠르게 원주좌표계를 계산을 끝내자.

앞에는 알겠는데
뒤에는 조금 낯설수도

x^2+y^2 앞에 계수가 양수니까
전체적인 형태는 아래로 볼록일 거고
(x,y)=(0,0)을 대입해보면 z=-1을 지나니까
그 점을 지나면서 아래로 볼록!
그리고 계수가 2가 곱해져 있으니
계수가 1인 놈보다는 더 빠르게 증가할거다!
xy평면에서 그래프 그릴 때도
우리가 이미 알고있는 함수에서
차이점만 보완해서 그리듯
3차원에서도 당황하지말고
내가 알고 있는 큰 틀에 있는 함수를 떠올리자!

그리고 교선까지!
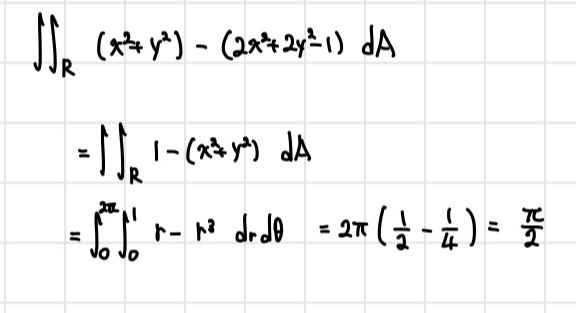
요놈도 원주좌표계로 빠르게 적분 끝.
0부터 1까지 적분은 알쥬?
아주 간단하게 호다닥 끝내기
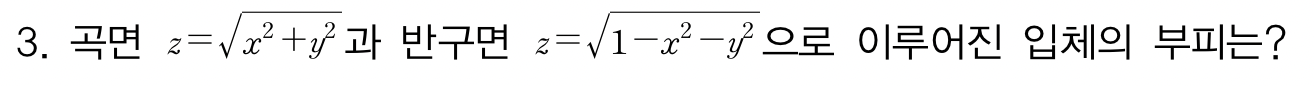
이제 반원형태를 함수로 주면
호다닥 그리듯
우리는 반구의 저 루트 형태에도 익숙해지자~
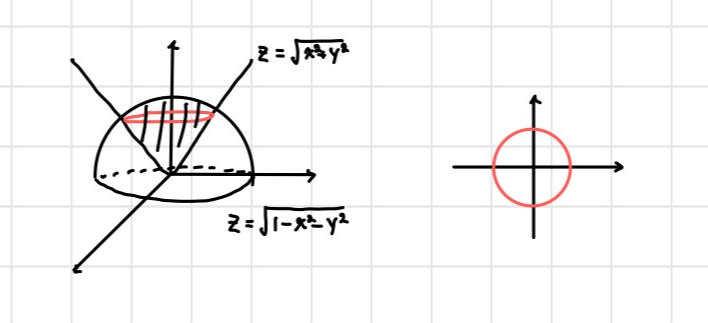
이건 나중에 구면좌표계로 더
빠르게 구할 수 있다~

이 교선을 가지고 적분을 해주면

반구는 원주좌표계를 이용했을때
루트가 사라지지 않아서
앞 2문제보다는 적분이 조금 더럽지만
못할 정도는 아니다~
나중엔 삼중적분으로도 부피를 구하게 되는데
개인적으로 이중적분을 잘하면 그 때
도움이 굉장히 된다고 생각!
그 때 가면 얘는 3중적분으로 부피 구하고
쟤는 2중적분으로 부피 구하고
지 맘대로 하는듯 보일 수 있는데
범위랑 함수형태를 보고 결정해야해서ㅜ
'수학 > 다변수' 카테고리의 다른 글
| 쌍곡면, 쌍곡면+구 부피구하기 (0) | 2024.05.11 |
|---|---|
| 이중적분 여러개를 하나로!(적분영역 합치기) (0) | 2023.09.04 |
| 이중적분과 이상적분[암기하는 적분형태] (0) | 2023.08.31 |
| 이중적분 적분범위 바꾸기 dydx, dxdy (0) | 2023.08.30 |
| 절댓값이 포함된 이중적분 (0) | 2023.08.29 |



